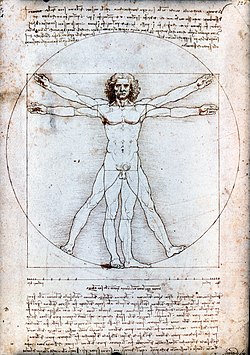
Ο Άνθρωπος του Βιτρούβιου

 Ο Άνθρωπος του Βιτρούβιου είναι διάσημο σχέδιο με συνοδευτικές σημειώσεις του Λεονάρντο ντα Βίντσι, που φτιάχτηκε περίπου το 1490 σε ένα από τα ημερολόγιά του. Απεικονίζει μία φιγούρα σε δύο αλληλοκαλυπτόμενες θέσεις με τα μέλη του ανεπτυγμένα και συγχρόνως εγγεγραμμένη σε ένα κύκλο και ένα τετράγωνο. Το σχέδιο και το κείμενο συχνά ονομάζονται Κανόνας των Αναλογιών.

Ο Άνθρωπος του Βιτρούβιου
Λεονάρντο ντα Βίντσι
έτος: 1487

Σύμφωνα με τις σημειώσεις του ντα Βίντσι στο συνοδευτικό κείμενο, οι οποίες είναι γραμμένες με καθρεπτιζόμενη γραφή, το σχέδιο έγινε ως μελέτη των αναλογιών του (ανδρικού) ανθρώπινου σώματος όπως περιγράφεται σε μια πραγματεία του Ρωμαίου αρχιτέκτονα Βιτρούβιου, που είχε γράψει για το ανθρώπινο σώμα:

• μια παλάμη έχει πλάτος τεσσάρων δακτύλων
• ένα πόδι έχει πλάτος τέσσερις παλάμες
• ένας πήχυς έχει πλάτος έξι παλάμες
• το ύψος ενός ανθρώπου είναι τέσσερις πήχεις (και άρα 24 παλάμες)
• μια δρασκελιά είναι τέσσερις πήχεις
• Το μήκος των χεριών ενός άντρα σε διάταση είναι ίσο με το ύψος του
• η απόσταση από την γραμμή των μαλλιών ως την κορυφή του στήθους είναι το ένα-έβδομο του ύψους του άνδρα
• η απόσταση από την κορυφή του κεφαλιού ως τις θηλές είναι το ένα-τέταρτο του ύψους του άνδρα
• το μέγιστο πλάτος των ώμων είναι το ένα-τέταρτο του ύψους του άνδρα
• η απόσταση από τον αγκώνα ως την άκρη του χεριού είναι το ένα-πέμπτο του ύψους του άνδρα
• η απόσταση από τον αγκώνα ως την μασχάλη είναι το ένα-όγδοο του ύψους του άνδρα
• η απόσταση από την άκρη του πηγουνιού ως την μύτη είναι το ένα-τρίτο του μήκους του προσώπου
• η απόσταση της γραμμής των μαλλιών ως τα φρύδια είναι το ένα-τρίτο του μήκους του προσώπου
• το μήκος του αυτιού είναι το ένα-τρίτο του μήκους του προσώπου
• το μήκος του αντίχειρα ενός ανθρώπου είναι ίσο με το μήκος της μύτης του

Φαίνεται ότι ο ντα Βίντσι δημιούργησε το σχέδιο βασιζόμενος στο De Architectura 3.1.3 του Βιτρούβιου που γράφει:

Ο ομφαλός είναι φυσικά τοποθετημένος στο κέντρου του ανθρώπινου σώματος, και, αν σε έναν άνδρα ξαπλωμένο, με το πρόσωπο στραμμένο επάνω και τα χέρια και τα πόδια του ανεπτυγμένα, με τον ομφαλό του ως κέντρο εγγράψουμε ένα κύκλο, θα ακουμπήσει τα δάκτυλα των χεριών και τα δάκτυλα των ποδιών του. Δεν γίνεται μόνο μέσω ενός κύκλου, η περιγραφή ενός ανθρώπινου σώματος, όπως φαίνεται τοποθετώντας τον σε ένα τετράγωνο. Μετρώντας από τα πόδια ως στην κορυφή του κεφαλιού, και έπειτα κατά μήκος των χεριών σε πλήρη έκταση, βρίσκουμε την τελευταία μέτρηση ίση με την πρώτη· έτσι γραμμές σε ορθή γωνία μεταξύ τους, περικλείοντας τη φιγούρα, σχηματίζουν ένα τετράγωνο.

Μία άλλη πηγή έμπνευσης για τον Βιτρούβιο Άντρα του ντα Βίντσι ήταν και ο Παγκόσμιος Άνθρωπος της Χίλντεγκαρντ του Μπίνγκεν η οποία σίγουρα θα ήταν και εκείνη εξοικειωμένη με το έργο του Βιτρούβιου.

Η επαναφορά των ανακαλύψεων των μαθηματικών αναλογιών του ανθρώπινου σώματος τον 15ο αιώνα από τον ντα Βίντσι και άλλους θεωρείται ένα από τα μεγάλα επιτεύγματα που οδήγησαν στην Ιταλική Αναγέννηση. Το σχέδιο του ντα Βίντσι συνδυάζει μια προσεκτική ανάγνωση του αρχαίου κειμένου με τις δικές του παρατηρήσεις σε αληθινά ανθρώπινα σώματα. Κατά το σχεδιασμό του κύκλου και του τετραγώνου πολύ σωστά παρατήρησε ότι το τετράγωνο δεν μπορεί να έχει το ίδιο κέντρο με τον κύκλο, στον ομφαλό, αλλά κάπου χαμηλότερα στην ανατομία. Αυτή η ρύθμιση είναι μια καινοτομία στο σχέδιο του ντα Βίντσι και το ξεχωρίζει από προγενέστερες απεικονίσεις.

Το ίδιο το σχέδιο συχνά χρησιμοποιείται ως ένα υπονοούμενο σύμβολο της ουσιώδους συμμετρίας του ανθρώπινου σώματος, και κατά προέκταση του Σύμπαντος ως συνόλου.

Μπορεί να παρατηρηθεί από την εξέταση του σχεδίου ότι ο συνδυασμός των θέσεων των χεριών και των ποδιών μπορεί να δημιουργήσει δεκαέξι διαφορετικές στάσεις. Η στάση με τα χέρια εκτεταμένα μακριά και τα πόδια ενωμένα είναι εγγεγραμμένη στο τετράγωνο. Η στάση με τα χέρια ελαφρώς υψωμένα και τα πόδια ανοικτά εγγράφεται στον κύκλο. Αυτό εικονογραφεί το θεώρημα ότι κατά την εναλλαγή μεταξύ των δύο στάσεων, το φαινόμενο κέντρο της φιγούρας φαίνεται να κινείται, αλλά στην πραγματικότητα ο ομφαλός της φιγούρας που είναι το πραγματικό κέντρο της βαρύτητας παραμένει ακίνητος.